
80%的考生不知道,丢分真凶不是计算能力,而是思维断点
每年高考数学结束,总有一群学生捶胸顿足:“圆锥曲线大题又算崩了!”一张张草稿纸写满凌乱的算式,时间耗尽却得不出正确答案。数据显示,高考中圆锥曲线综合题平均得分率不足45%,成为拉开分数差距的“头号杀手”79。一线教学18年的数学名师张培锋直言:“丢分本质不是算力不足,而是思维链条存在致命裂缝。”
一、三大高频失分点,你掉进了哪个坑?
1. 定义域遗忘——隐形的地雷
-
典型案例:求双曲线 $x^2/9 – y^2/4 = 1$ 与直线 $y = kx + 1$ 的交点,未限定 $|k| > 2/3$ 导致增解3。
-
破局钥匙:联立方程后必先确认 $\Delta ≥ 0$!双曲线需额外验证渐近线斜率(如 $|k| > b/a$),椭圆需关注隐含范围(如 $-a ≤ x ≤ a$)610。
2. “设而不求”失效——计算沼泽的源头
-
惨痛教训:弦长问题硬求 $x_1, x_2$ 坐标,陷入根式化简泥潭1。
-
黄金法则:牢记 “三部曲”套路:一设(直线方程)、二联立(口算判别式)、三韦达定理(活用 $x_1 + x_2$, $x_1 x_2$)。如弦长公式直接转化为 $\sqrt{1 + k^2} \cdot \frac{\sqrt{\Delta}}{|a|}$,省去70%运算量14。
3. 几何性质忽略——压轴题的致命盲区
-
真实案例:2023年新课标II卷压轴题,若发现 焦点三角形 中 $\angle P F_1 F_2 = 90^\circ$,可秒用 $|PF_1|^2 + |PF_2|^2 = 4c^2$,否则需耗15分钟推导710。
-
必背工具:椭圆中 $S_{\triangle PF_1 F_2} = b^2 \tan \frac{\theta}{2}$($\theta$ 为顶角);抛物线 焦点弦长 $|AB| = \frac{2p}{\sin^2 \alpha}$($\alpha$ 为倾斜角)58。
二、四招实战技巧,逆袭考场时间刺客
▶ 点差法:中点弦问题的核武器
-
操作口诀:“设点-作差-代斜率”。已知弦中点 $M(x_0, y_0)$ 时,对双曲线 $\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1$ 有 $\frac{y_0}{x_0} = \frac{b^2}{a^2} \cdot k_{弦}$,避免联立方程34。
-
真题应用:若椭圆 $\frac{x^2}{16} + \frac{y^2}{9} = 1$ 弦中点 $M(2, 1)$,则 $k_{弦} = -\frac{9 \times 2}{16 \times 1} = -\frac{9}{8}$,10秒出结果4。
▶ 降维打击:参数方程巧破最值
-
场景:求椭圆上点 $P$ 到直线 $l$ 距离最值。直角坐标需导函数求极值,而参数方程 $P(4\cos\theta, 3\sin\theta)$ 直接化归 $d = \frac{|4\cos\theta – 3\sin\theta + 6|}{\sqrt{5}}$,三角函数辅助角公式速解59。
▶ 错题本活性管理:从“死抄”到“动态攻防”
-
星级诊断法:
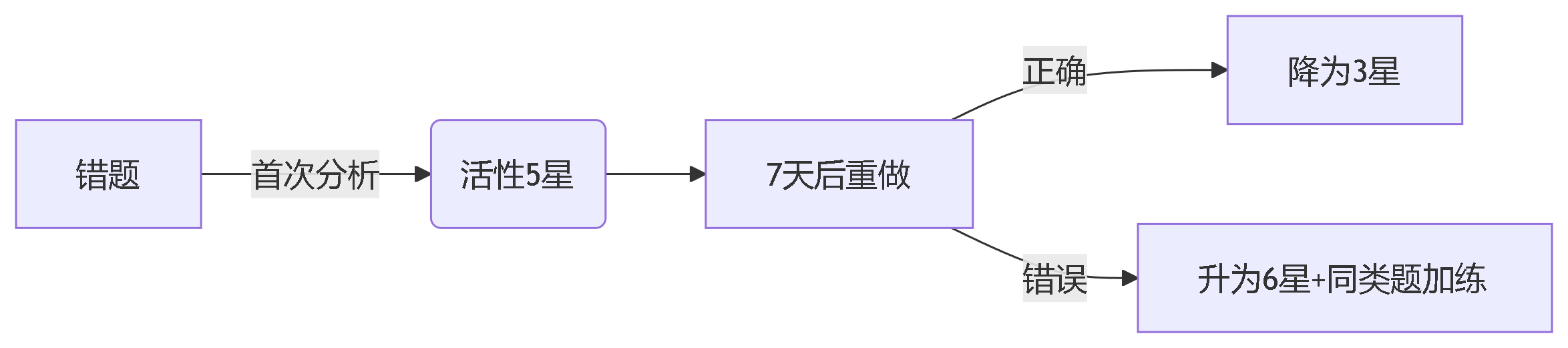
-
2024届考生李某用此法将离心率范围类错题活性值从4.8星降至1.2星,正确率提升至89%46。
▶ 考场急救包:三类二级结论
-
切线定理:椭圆 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ 在 $P(x_0, y_0)$ 处切线为 $\frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} = 1$
-
焦半径比例:抛物线 $y^2 = 2px$ 焦点弦 $AB$ 满足 $\frac{1}{|AF|} + \frac{1}{|BF|} = \frac{2}{p}$
-
定比点差:向量题中若 $\overrightarrow{AP} = \lambda \overrightarrow{PB}$,则 $x_1 – \lambda x_2 = x_A – \lambda x_B$($y$ 坐标同理)57
三、三轮复习引擎,打造解题肌肉记忆
▷ 基础扫雷阶段(30天)
-
每天精练1道 “定义-方程-几何性质”三位一体题,例如:“已知双曲线离心率 $e = 2$,渐近线夹角 $\theta$,求 $\cos \theta$ 范围”,强化 定义域敏感度610。
▷ 模块突破阶段(45天)
-
按 中点弦/定点定值/轨迹问题 分类刷题,推荐“3+1”模式:3道通解训练(点差法+韦达定理)+1道几何法巧解(如利用 垂径定理 或 对称性)89。
▷ 压轴冲刺阶段(15天)
-
对 探索性问题(如“是否存在点 $P$ 使 $\angle APB = 90^\circ$”)建立 假设-验证-特例 三步骤,尤其重视 特殊位置法(取顶点、焦点)57。
高考命题人视角:圆锥曲线压轴题的本质是 “几何条件代数化”。若解题步骤超过10行,必有可简化的思维跳步。
备考终极箴言
-
草稿分区术:将草稿纸对折成4宫格,每区标题型(如“定义域”“韦达转化”),步骤断层处红笔圈出4;
-
5分钟法则:单步计算超时立即跳转下一问,高考题设计具有 关联独立性,后问或可反哺前问9;
-
命题反推法:拆解真题答案,标注 “命题陷阱点”(如“此处需讨论斜率不存在”),培养出题人思维710。
当你能在10分钟内完成一道 椭圆与向量综合题,当 点差法 成为肌肉记忆,当错题本的 活性值 趋近于零——曾经令人生畏的 圆锥曲线,终将成为你冲刺140+的 黄金阶梯。高分从来不是天赋者的专利,而是策略者的战利品。
原文链接:http://www.xkw123.cn/3248/,转载请注明出处。





评论0